1.3 Matrices, Determinants, and the Cross Product
In Section 1.2 we defined a product of vectors that was a scalar. In this section we shall define a product of vectors that is a vector; that is, we shall show how, given two vectors \({\bf a}\) and \({\bf b}\), we can produce a third vector \({\bf a}\times {\bf b}\), called the cross product of a and b. This new vector will have the pleasing geometric property that it is perpendicular to the plane spanned (determined) by \({\bf a}\) and \({\bf b}\). The definition of the cross product is based on the notions of the matrix and the determinant, and so these are developed first. Once this has been accomplished, we can study the geometric implications of the mathematical structure we have built.
\(2\times 2\,\) Matrices
We define a \(2\,{\times}\,2\) matrix to be an array \[ \bigg[ \begin{array} &a_{11} & a_{12}\\ a_{21} & a_{22} \end{array} \bigg], \] where \(a_{11},a_{12},a_{21}\), and \(a_{22}\) are four scalars. For example, \[ \bigg[ \begin{array} &2 & 1\\ 0 & 4 \end{array} \bigg], \bigg[ \begin{array} &{-}1 &0\\ 1 & 1 \end{array} \bigg],\qquad\hbox{and}\qquad\bigg[\begin{array} &13 &7\\ 6 & 11 \end{array} \bigg] \] are \(2\times 2\) matrices. The determinant \[ \left| \begin{array} &a_{11} & a_{12}\\ a_{21} & a_{22} \end{array} \right| \] of such a matrix is the real number defined by the equation \[ \bigg| \begin{array} &a_{11} & a_{12}\\ a_{21} & a_{22} \end{array} \bigg| =a_{11}a_{22} - a_{12} a_{21}.\tag{1} \]
example 1
\[ \bigg| \begin{array} &1 & 1 \\ 1 & 1 \end{array} \bigg|=1-1=0;\qquad \bigg|\begin{array} &1 & 2 \\ 3 & 4 \end{array} \bigg| =4-6=-2;\qquad \bigg| \begin{array} &5 & 6\\ 7 & 8 \end{array} \bigg| =40-42=-2 \]
\(3\times 3\,\) Matrices
A \(3\,{\times}\,3\) matrix is an array \[ \left[ \begin{array}{@{}c@{\quad}c@{\quad}c@{}} a_{11} & a_{12} & a_{13}\\ a_{21} & a_{22} & a_{23}\\ a_{31} & a_{32} & a_{33} \end{array} \right], \]
32
where, again, each \(a_{ij}\) is a scalar; \(a_{ij}\) denotes the entry in the array that is in the \(i\)th row and the \(j\)th column. We define the determinant of a \(3\times 3\) matrix by the rule \begin{equation} \left| \begin{array}{@{}c@{\quad}c@{\quad}c@{}} a_{11} & a_{12} & a_{13}\\ a_{21} & a_{22} & a_{23}\\ a_{31} & a_{32} & a_{33} \end{array} \right| =a_{11} \bigg| \begin{array} a_{22} & a_{23} \\ a_{32} & a_{33} \end{array}\bigg| -a_{12} \bigg| \begin{array} a_{21} & a_{23} \\[.6pt] a_{31} & a_{33} \end{array}\bigg| +a_{13} \bigg| \begin{array} a_{21} & a_{22} \\[.6pt] a_{31} & a_{32} \end{array}\bigg|.\tag{2} \end{equation}
Without some mnemonic device, formula (2) would be difficult to memorize. The rule to learn is that you move along the first row, multiplying \(a_{{\rm 1}j}\) by the determinant of the \(2\times 2\) matrix obtained by canceling out the first row and the \(j\)th column, and then you add these up, remembering to put a minus in front of the \(a_{12}\) term. For example, the determinant multiplied by the middle term of formula (2), namely, \[ \bigg| \begin{array} &a_{21} & a_{23} \\ a_{31} & a_{33} \end{array} \bigg|, \] is obtained by crossing out the first row and the second column of the given \(3\times 3\) matrix: \[ \left[ \begin{array} \sout{\rlap{ }} a_{11} & a_{12} &a_{13}\\ a_{21} & a_{22} \smash{\llap{ \quad}} &a_{23}\\ a_{31} & a_{32} &a_{33} \end{array}\right]. \]
example 2
\begin{eqnarray*} & \left| \begin{array} &1 & 0 & 0\\ 0 & 1 & 0\\ 0 & 0 & 1 \end{array} \right|=1\, \bigg| \begin{array} &1 & 0 \\ 0 & 1 \end{array} \bigg|-0\, \bigg| \begin{array} &0 & 0 \\ 0 &1 \end{array} \bigg|+0\, \bigg| \begin{array} &0 & 1 \\ 0 & 0 \end{array} \bigg| =1. \\ & \left| \begin{array} &1 & 2 & 3\\ 4 & 5 & 6\\ 7 & 8 & 9 \end{array} \right|=1\, \bigg| \begin{array} &5 & 6 \\ 8& 9 \end{array} \bigg|-2\, \bigg|\begin{array} &4 & 6 \\ 7 &9 \end{array} \bigg| +3\, \bigg| \begin{array} &4 & 5\\ 7 & 8 \end{array} \bigg|=-3 + 12-9=0 \\ \end{eqnarray*}
Properties of Determinants
An important property of determinants is that interchanging two rows or two columns results in a change of sign. For \(2\times 2\) determinants, this is a consequence of the definition as follows: For rows, we have \begin{eqnarray*} \bigg| \begin{array} &a_{11} & a_{12}\\ a_{21} & a_{22} \end{array} \bigg| =a_{11} a_{22}-a_{21}a_{12} =-(a_{21} a_{12} - a_{11} a_{22}) = -\bigg| \begin{array} &a_{21} & a_{22} \\ a_{11} & a_{12} \end{array} \bigg| \end{eqnarray*} and for columns, \[ \bigg| \begin{array} &a_{11} & a_{12} \\ a_{21} & a_{22} \end{array} \bigg| = -( a_{12} a_{21} - a_{11} a_{22} ) = - \bigg| \begin{array} &a_{12} & a_{11} \\ a_{22} & a_{21} \end{array} \bigg|. \] We leave it to you to verify this property for the \(3\times 3\) case.
A second fundamental property of determinants is that we can factor scalars out of any row or column. For \(2\times 2\) determinants, this means \[ \bigg|\begin{array} &\alpha a_{11} & a_{12} \\ \alpha a_{21} & a_{22} \end{array} \bigg| = \bigg|\begin{array} &a_{11} & \alpha a_{12} \\ a_{21} & \alpha a_{22} \end{array} \bigg| = \alpha \bigg|\begin{array} &a_{11} & a_{12} \\ a_{21} & a_{22} \end{array} \bigg| = \bigg|\begin{array}{@{}r@{\quad}r@{}} \alpha a_{11} & \alpha a_{12} \\ a_{21} & a_{22} \end{array} \bigg| = \bigg|\begin{array}{@{}r@{\quad}r@{}} a_{11} & a_{12} \\ \alpha a_{21} & \alpha a_{22} \end{array} \bigg|. \]
33
Similarly, for \(3 \times 3\) determinants we have \[ \left|\begin{array}{@{}r@{\quad}r@{\quad}r@{}} \alpha a_{11} & \alpha a_{12} & \alpha a_{13} \\ a_{21} & a_{22} & a_{23} \\ a_{31} & a_{32} & a_{33} \end{array} \right| \,=\, \alpha \left|\begin{array}{@{}c@{\quad}c@{\quad}c@{}} a_{11} & a_{12} & a_{13} \\ a_{21} & a_{22} & a_{23} \\ a_{31} & a_{32} & a_{33} \end{array} \right| \,=\, \left|\begin{array}{@{}c@{\quad}c@{\quad}c@{}} a_{11} & \alpha a_{12} & a_{13} \\ a_{21} & \alpha a_{22} & a_{23} \\ a_{31} & \alpha a_{32} & a_{33} \end{array} \right|\kern-2pt, \] and so on. These results follow from the definitions. In particular, if any row or column consists of zeros, then the value of the determinant is zero.
A third fundamental fact about determinants is the following: If we change a row (or column) by adding another row (or, respectively, column) to it, the value of the determinant remains the same. For the \(2\times 2\) case, this means that \begin{eqnarray*} \bigg|\begin{array} &a_1 & a_2 \\ b_1 & b_2 \end{array} \bigg| &=& \bigg|\begin{array} &a_1 + b_1 & a_2 + b_2 \\ b_1 & b_2 \end{array} \bigg| = \bigg|\begin{array} &a_1 & a_2 \\ b_1 + a_1 & b_2 + a_2 \end{array} \bigg| \\[4pt] & = & \bigg|\begin{array} &a_1 + a_2 & a_2 \\ b_1 + b_2 & b_2 \end{array} \bigg| = \bigg|\begin{array} &a_1 & a_1 + a_2 \\ b_1 & b_1 + b_2 \end{array} \bigg|. \end{eqnarray*}
For the \(3 \times 3\) case, this means \[ \left|\begin{array}{@{}c@{\quad}c@{\quad}c@{}} a_1 & a_2 & a_3 \\ b_1 & b_2 & b_3 \\ c_1 & c_2 & c_3 \end{array} \right| = \left|\begin{array}{@{}c@{\quad}c@{\quad}c@{}} a_1 + b_1 & a_2 + b_2 & a_3 + b_3 \\ b_1 & b_2 & b_3 \\ c_1 & c_2 & c_3 \end{array} \right|= \left|\begin{array}{@{}c@{\quad}c@{\quad}c@{}} a_1 + a_ 2 & a_2 & a_3 \\ b_1 + b_2 & b_2 & b_3 \\ c_1 + c_2 & c_2 & c_3 \end{array} \right|\kern-2pt, \] and so on. Again, this property can be proved using the definition of the determinant.
example 3
Suppose \[ {\bf a} = \alpha {\bf b} + \beta {\bf c};\hbox{that is, } {\bf a} = (a_1, a_2, a_3) = \alpha (b_1, b_2, b_3) + \beta (c_1, c_2, c_3). \]
Show that \[ \left|\begin{array}{@{}c@{\quad}c@{\quad}c@{}} a_1 & a_2 & a_3 \\ b_1 & b_2 & b_3 \\ c_1 & c_2 & c_3 \end{array} \right| =0. \]
solution We shall prove the case \(\alpha \neq 0,\beta \neq 0\). The case \(\alpha = 0 =\beta\) is trivial, and the case where exactly one of \(\alpha , \beta\) is zero is a simple modification of the case we prove. Using the fundamental properties of determinants, the determinant in question is \begin{eqnarray*} \begin{array}{l} \left|\begin{array}{@{}c@{\quad}c@{\quad}c@{}} \alpha b_1 + \beta c_1 & \alpha b_2 + \beta c_2 & \alpha b_3 + \beta c_3 \\ b_1 & b_2 & b_3 \\ c_1 & c_2 & c_3 \end{array} \right|\\[2pc] \qquad = {} -\kern-2pt{\displaystyle \frac{1}{\alpha}} \left|\begin{array}{@{}c@{\quad}c@{\quad}c@{}} \alpha b_1 + \beta c_1 & \alpha b_2 + \beta c_2 & \alpha b_3 + \beta c_3 \\ - \alpha b_1 & - \alpha b_2 & - \alpha b_3 \\ c_1 & c_2 & c_3 \end{array} \right| \\[15pt] \hbox{ (factoring } {-}1 / \alpha \hbox{ out of the second row)} \\[12pt] \qquad ={} \bigg( -\kern-2pt\displaystyle\frac{1}{\alpha} \bigg) \bigg( -\kern-2pt\displaystyle\frac{1}{\beta} \bigg) \left|\begin{array}{@{}c@{\quad}c@{\quad}c@{}} \alpha b_1 + \beta c_1 & \alpha b_2 + \beta c_2 & \alpha b_3 + \beta c_3 \\ - \alpha b_1 & - \alpha b_2 & - \alpha b_3 \\ - \beta c_1 & - \beta c_2 & - \beta c_3 \end{array} \right| \\[15pt] \hbox{(factoring } {-}1 / \beta \hbox{ out of the third row)}\\[-24pt] \end{array} \end{eqnarray*}
\begin{eqnarray*} \begin{array}{l} \qquad = {} \frac{1}{\alpha \beta} \left|\begin{array}{@{}c@{\quad}c@{\quad}c@{}} \beta c_1 & \beta c_2 & \beta c_3 \\ - \alpha b_1 & - \alpha b_2 & - \alpha b_3 \\ - \beta c_1 & - \beta c_2 & - \beta c_3 \end{array} \right|\qquad \hbox{ (adding the second row to the first row)} \\[2pc] \qquad = {} \frac{1}{\alpha \beta} \left|\begin{array}{@{}c@{\quad}c@{\quad}c@{}} 0 & 0 & 0 \\ - \alpha b_1 & - \alpha b_2 & - \alpha b_3 \\ - \beta c_1 & - \beta c_2 & - \beta c_3 \end{array} \right| \qquad \hbox{ (adding the third row to the first row)} \\[18pt] \qquad ={} 0. \end{array} \end{eqnarray*}
34
Closely related to these properties is the fact that we can expand a \(3\times 3\) determinant along any row or column using the signs in the following checkerboard pattern: \[ \left|\begin{array}{@{}c@{\quad}c@{\quad}c@{}} + & - & + \\ - & + & - \\ + & - & + \end{array} \right| \]
For instance, you can check that we can expand “by minors” along the middle row: \[ \left|\begin{array}{@{}c@{\quad}c@{\quad}c@{}} a_{11} & a_{12} & a_{13} \\ a_{21} & a_{22} & a_{23} \\ a_{31} & a_{32} & a_{33} \end{array} \right| = -a_{21} \left|\begin{array} &a_{12} & a_{13}\\ \\ a_{32} & a_{33} \end{array}\right| + a_{22} \left|\begin{array} &a_{11} & a_{13}\\ \\ a_{31} & a_{33} \end{array}\right| - a_{23} \left|\begin{array} &a_{11} & a_{12}\\ \\ a_{31} & a_{32} \end{array}\right|. \]
Let us redo the second determinant in Example 2 using this formula: \[ \hskip-1.6pt\left|\begin{array}{@{}c@{\quad}c@{\quad}c@{}} 1 & 2 & 3 \\ 4 & 5 & 6 \\ 7 & 8 & 9 \end{array} \right| \hskip-.1pt = - 4 \left|\begin{array}{@{}c@{\quad \hskip-.3pt}c@{}} 2 & 3 \\ \\ 8 & 9 \end{array} \right| + 5 \left|\begin{array}{@{}c@{\quad \hskip-.3pt}c@{}} 1 & 3 \\ \\ 7 & 9 \end{array}\right| - 6 \left|\begin{array}{@{}c@{\quad \hskip-.3pt}c@{}} 1 & 2 \\ \\ 7 & 8 \end{array}\right| = (-4)(-6)+(5)(12) + (-6)(6) =0. \]
Historical Note
Determinants appear to have been invented and first used by Leibniz in 1693, in connection with solutions of linear equations. Maclaurin and Cramer developed their properties between 1729 and 1750; in particular, they showed that the solution of the system of equations \begin{eqnarray*} a_{\;11} x_{\;1} + a_{\;12} x_{\;2} + a_{\;13} x_3 = b_{\;1} \\ a_{\;21} x_{\;1} + a_{\;22} x_{\;2} + a_{\;23} x_3 = b_{\;2} \\ a_{\;31} x_{\;1} + a_{\;32} x_{\;2} + a_{\;33} x_3 = b_{\;3} \end{eqnarray*} is \[ \hskip5ptx_1\kern-1pt=\kern-1pt\frac{1}{\Delta}\kern-1pt \left|\begin{array}{@{}c@{\hskip9pt}c@{\hskip9pt}c@{}} b_{\;1} & a_{\;12} & a_{\;13} \\ b_{\;2} & a_{\;22} & a_{\;23} \\ b_{\;3} & a_{\;32} & a_{\;33} \end{array} \right|\kern-2pt, \qquad\hskip-3ptx_2\kern-1pt=\kern-1pt\frac{1}{\Delta}\kern-1pt \left|\begin{array}{@{}c@{\hskip9pt}c@{\hskip9pt}c@{}} a_{\;11} & b_{\;1} & a_{\;13} \\ a_{\;21} & b_{\;2} & a_{\;23} \\ a_{\;31} & b_{\;3} & a_{\;33} \end{array} \right|\kern-2pt, \qquad\hskip-3ptx_3 \,{=}\, \frac{1}{\Delta}\kern-1pt \left|\begin{array}{@{}c@{\hskip9pt}c@{\hskip9pt}c@{}} a_{\;11} & a_{\;12} & b_{\;1} \\ a_{\;21} & a_{\;22} & b_{\;2} \\ a_{\;31} & a_{\;32} & b_{\;3} \end{array} \right|, \] where \[ \Delta = \left|\begin{array}{@{}c@{\hskip9pt}c@{\hskip9pt}c@{}} a_{\;11} & a_{\;12} & a_{\;13} \\ a_{\;21} & a_{\;22} & a_{\;23} \\ a_{\;31} & a_{\;32} & a_{\;33} \end{array} \right|\kern-2pt, \]
35
a fact now known as Cramer’s rule. While this method is rather inefficient from a numerical point of view, it is of theoretical importance in matrix theory. Later, Vandermonde (1772) and Cauchy (1812), treating determinants as a separate topic worthy of special attention, developed the field more systematically, with contributions by Laplace, Jacobi, and others. Formulas for volumes of parallelepipeds in terms of determinants are due to Lagrange (1775). We shall study these later in this section. Although during the nineteenth century mathematicians studied matrices and determinants, the subjects were considered to be distinct disciplines. For the full history up to 1900, see T. Muir, The Theory of Determinants in the Historical Order of Development (reprinted by Dover, New York, 1960).
Cross Products
Now that we have established the necessary properties of determinants and discussed their history, we are ready to proceed with the cross product of vectors.
Definition: The Cross Product
Suppose that \({\bf a} = a_1 {\bf i} + a_2 {\bf j} + a_3 {\bf k}\) and \({\bf b} = b_1 {\bf i} + b_2 {\bf j} + b_3 {\bf k}\) are vectors in \({\mathbb R}^3\). The cross product or vector product of \({\bf a}\) and \({\bf b},\) denoted \({\bf a}\times {\bf b}\), is defined to be the vector \[ {\bf a} \times {\bf b} = \bigg|\begin{array} &a_2 & a_3 \\ b_2 & b_3 \end{array} \bigg|\, {\bf i} - \bigg|\begin{array} &a_1 & a_3 \\ b_1 & b_3 \end{array} \bigg| \,{\bf j} + \bigg|\begin{array} &a_1 & a_2 \\ b_1 & b_2 \end{array} \bigg|\, {\bf k}, \] or, symbolically, \[ {\bf a} \times {\bf b} = \left|\begin{array}{@{}c@{\quad}c@{\quad}c@{}} {\bf i } & {\bf j} & {\bf k} \\[1pt] a_1 & a_2 & a_3 \\[1pt] b_1 & b_2 & b_3 \end{array} \right|. \]
Even though we only defined determinants for arrays of real numbers, this formal expression involving vectors is a useful memory aid for the cross product.
example 4
Find \(( 3 {\bf i} - {\bf j} + {\bf k}) \times ( {\bf i} + 2 {\bf j} - {\bf k}).\)
solution
\[ ( 3 {\bf i} - {\bf j} + {\bf k}) \times ( {\bf i} + 2 {\bf j} - {\bf k}) = \left|\begin{array}{@{}c@{\quad}r@{\quad}r@{}} {\bf i} & {\bf j} & {\bf k} \\ 3 & -1 & 1 \\ 1 & 2 & -1 \end{array} \right| = - {\bf i} + 4 {\bf j} + 7 {\bf k}. \]
Certain algebraic properties of the cross product follow from the definition. If a, b, and c are vectors and \(\alpha\), \(\beta\), and \(\gamma\) are scalars, then
- (i) \({\bf a} \times {\bf b} = - ( {\bf b} \times {\bf a})\)
- (ii) \({\bf a} \times ( \beta {\bf b} + \gamma {\bf c}) = \beta ( {\bf a} \times {\bf b} ) + \gamma ( {\bf a} \times {\bf c}) \hbox{ and } (\alpha {\bf a} + \beta {\bf b}) \times {\bf c} = \alpha ( {\bf a} \times { \bf c}) + \beta ( {\bf b} \times {\bf c})\).
Note that \({\bf a} \times {\bf a} = - ( {\bf a} \times {\bf a})\), by property (i). Thus, \({\bf a} \times {\bf a} ={\bf 0}\). In particular, \[ {\bf i} \times {\bf i} ={\bf 0} ,\qquad {\bf j} \times {\bf j} ={\bf 0}, \qquad {\bf k} \times {\bf k} ={\bf 0}. \]
36
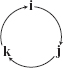
Also, \[ {\bf i} \times {\bf j} ={\bf k}, \qquad {\bf j} \times {\bf k} ={\bf i}, \qquad {\bf k} \times {\bf i} ={\bf j}, \] which can be remembered by cyclicly permuting \({\bf i,j,k}\) like this:
To give a geometric interpretation of the cross product, we first introduce the triple product. Given three vectors \({\bf a},{\bf b}\), and \({\bf c}\), the real number \[ ({\bf a}\times {\bf b})\,{\cdot}\, {\bf c} \] is called the triple product of \({\bf a},{\bf b}\), and \({\bf c}\) (in that order). To obtain a formula for it, let \({\bf a} = a_1 {\bf i} + a_2 {\bf j} + a_3 {\bf k}, {\bf b} = b_1 {\bf i} + b_2 {\bf j} + b_3 {\bf k}\), and \({\bf c} = c_1 {\bf i} + c_2 {\bf j} + c_3 {\bf k}\). Then \begin{eqnarray*} ({\bf a} \times {\bf b}) \,{\cdot}\, {\bf c}&=& \bigg( \bigg|\begin{array} &a_2 & a_3 \\ b_2 & b_3 \end{array} \bigg|\, {\bf i} - \bigg|\begin{array} &a_1 & a_3 \\ b_1 & b_3 \end{array} \bigg|\, {\bf j} + \bigg|\begin{array} &a_1 & a_2 \\ b_1 & b_2 \end{array} \bigg|\, {\bf k} \bigg) \,{\cdot}\,(c_1{\bf i} +c_2{\bf j}+c_3{\bf k})\\[3pt] &=& \bigg|\begin{array} &a_2 & a_3 \\ b_2 & b_3 \end{array} \bigg|\,c_1 - \bigg|\begin{array} &a_1 & a_3 \\ b_1 & b_3 \end{array} \bigg|\,c_2 + \bigg|\begin{array} &a_1 & a_2 \\ b_1 & b_2 \end{array} \bigg|\,c_3. \end{eqnarray*}
This is the expansion by minors of the third row of the determinant, so \[ ({\bf a} \times {\bf b}) \,{\cdot}\, {\bf c} = \left|\begin{array}{@{}c@{\quad}c@{\quad}c@{}} a_1 & a_2 & a_3 \\ b_1 & b_2 & b_3 \\ c_1 & c_2 & c_3 \end{array} \right|. \]
If c is a vector in the plane spanned by the vectors a and b, then the third row in the determinant expression for \(({\bf a}\times {\bf b})\,{\cdot}\, {\bf c} \) is a linear combination of the first and second rows, and therefore \(({\bf a }\times {\bf b})\,{\cdot}\, {\bf c}=0\). In other words, the vector \({\bf a} \times {\bf b}\) is orthogonal to any vector in the plane spanned by a and b, in particular to both \({\bf a}\) and \({\bf b}\).
Next, we calculate the length of \({\bf a}\times {\bf b}\). Note that \[ \begin{array}{rcl} \| {\bf a} \times {\bf b} \|^2 &=& \bigg|\begin{array} &a_2 & a_3 \\ b_2 & b_3 \end{array}\bigg|^2 + \bigg|\begin{array} &a_1 & a_3 \\ b_1 & b_3 \end{array} \bigg|^2 + \bigg|\begin{array} &a_1 & a_2 \\ b_1 & b_2 \end{array} \bigg|^2 \\[1pc] & = & ( a_2 b_3 - a_3 b_2 )^2 + ( a_1 b_3 - b_1 a_3)^2 + (a_1 b_2 - b_1 a_2)^2. \end{array} \]
If we expand the terms in the last expression, we can recollect them to give \[ (a^2_1+a^2_2+a^2_3)(b^2_1+b^2_2+b^2_3)-(a_1b_1+a_2 b_2+a_3 b_3)^2, \] which equals \[ \|{\bf a}\|^2\|{\bf b}\|^2-({\bf a}\,{\cdot}\, {\bf b})^2= \|{\bf a}\|^2\|{\bf b}\|^2-\|{\bf a}\|^2\|{\bf b}\|^2\cos^2 \theta =\|{\bf a}\|^2\|{\bf b}\|^2\sin^2\theta, \] where \(\theta\) is the angle between \({\bf a}\) and \({\bf b}, 0\leq \theta \leq \pi\). Taking square roots and using \(\sqrt{k^2}=|k|\), we find that \(\|{\bf a}\times {\bf b}\|=\|{\bf a}\|\|{\bf b}\| {\mid}{\sin}\, \theta{\mid}\).
Combining our results, we conclude that \({\bf a}\times {\bf b}\) is a vector perpendicular to the plane \({\cal P}\) spanned by \({\bf a}\) and \({\bf b}\) with length \(\|{\bf a}\|\| {\bf b}\|{\mid}{\sin}\,{\theta}{\mid}\). We see from Figure 1.45 that this length is also the area of the parallelogram (with base \(\|{\bf a}\|\) and height \(\| {\bf b}\sin \theta\|\)) spanned by \({\bf a}\) and \({\bf b}\). There are still two possible vectors that satisfy these conditions because there are two choices of direction that are perpendicular (or normal) to \({\cal P}\). This is clear from Figure 1.45, which shows the two choices \({\bf n}_1\) and \(-{\bf n}_1\) perpendicular to \({\cal P}\), with \(\|{\bf n}_1\|=\|{-}{\bf n}_1\|=\|{\bf a}\|\|{\bf b}\|{\mid}{\sin}\, {\theta}{\mid}\).
37
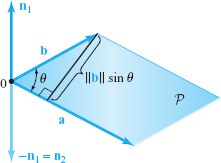
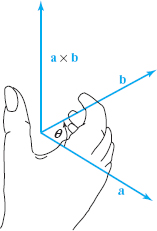
Which vector represents \({\bf a}\times {\bf b},{\bf n}_1\) or \({-}{\bf n}_1\)? The answer is \({\bf n}_1\). Try a few cases such as \({\bf k}={\bf i}\times {\bf j}\) to verify this. The following “right-hand rule” determines the direction of \({\bf a}\times {\bf b}\) in general. Take your right hand and place it so your fingers curl from \({\bf a}\) toward \({\bf b}\) through the acute angle \(\theta\), as in Figure 1.46. Then your thumb points in the direction of \({\bf a}\times {\bf b}\).
The Cross Product
Geometric definition: \({\bf a}\times {\bf b}\) is the vector such that:
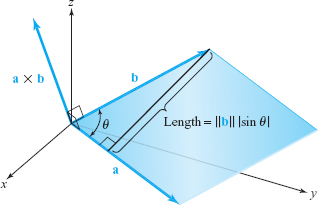
- \(\|{\bf a}\times {\bf b}\|=\|{\bf a}\|\|{\bf b}\|\sin \theta\), the area of the parallelogram spanned by \({\bf a}\) and \({\bf b}\) (\(\theta\) is the angle between \({\bf a}\) and \({\bf b}\);\(\,0\leq \theta\leq \pi\)); see Figure 1.47.
- \({\bf a}\times {\bf b}\) is perpendicular to \({\bf a}\) and \({\bf b}\), and the triple \(({\bf a},{\bf b},{\bf a}\times {\bf b})\) obeys the right-hand rule.
Component formula: \begin{eqnarray*} &&(a_1{\bf i}+a_2{\bf j}+a_3{\bf k})\times (b_1{\bf i}+b_2{\bf j}+b_3{\bf k})= \left|\begin{array}{@{}c@{\quad}c@{\quad}c@{}} {\bf i} & {\bf j} & {\bf k} \\ a_1 & a_2 & a_3 \\ b_1 & b_2 & b_3 \end{array} \right|\\[3pt] &&\quad{}=(a_2b_3-a_3b_2){\bf i}-(a_1b_3-a_3b_1){\bf j}+(a_1b_2-a_2b_1){\bf k}.\\[-20.6pt] \end{eqnarray*}
Algebraic rules:
- \({\bf a}\times {\bf b}={\bf 0}\) if and only if \({\bf a}\) and \({\bf b}\) are parallel or \({\bf a}\) or \({\bf b}\) is zero.
- \({\bf a}\times {\bf b}=-{\bf b}\times {\bf a}\).
- \({\bf a}\times ({\bf b}+{\bf c})={\bf a}\times {\bf b}+{\bf a}\times {\bf c}\).
- \(({\bf a}+{\bf b})\times {\bf c}={\bf a}\times {\bf c}+{\bf b}\times {\bf c}\).
- \((\alpha {\bf a})\times {\bf b}=\alpha ({\bf a}\times {\bf b})\).
Multiplication table:
| Second factor | ||||
| \(\times\) | i | j | k | |
| i | 0 | k | \(-\)j | |
| First | j | \(-\)k | 0 | i |
| factor | k | j | \(-\)i | 0 |
38
example 5
Find the area of the parallelogram spanned by the two vectors \({\bf a}={\bf i}\,+\,2{\bf j}\,+\,3{\bf k}\) and \({\bf b}=-{\bf i}-{\bf k}\).
solution We calculate the cross product of \({\bf a}\) and \({\bf b}\) by applying the component or determinant formula, with \(a_1=1\), \(a_2=2\), \(a_3=3\), \(b_1=-1\), \(b_2=0\), \(b_3\) \(=-1\): \begin{eqnarray*} {\bf a}\times {\bf b}&=&[(2)(-1)-(3)(0)]{\bf i}+[(3)(-1)-(1)(-1)] {\bf j}+[(1)(0)-(2)(-1)]{\bf k}\\ &=&-2{\bf i}-2{\bf j}+2{\bf k}. \end{eqnarray*}
Thus, the area is \[ \|{\bf a}\times {\bf b}\|=\sqrt{(-2)^2+(-2)^2+(2)^2}=2\sqrt{3}. \]
example 6
Find a unit vector orthogonal to the vectors \({\bf i}+{\bf j}\) and \({\bf j}+{\bf k}\).
solution A vector perpendicular to both \({\bf i}+{\bf j}\) and \({\bf j}+{\bf k}\) is their cross product, namely, the vector \[ ({\bf i}+{\bf j})\times (\,{\bf j}+{\bf k})=\left| \begin{array}{@{}c@{\quad}c@{\quad}c@{}} {\bf i} & {\bf j} & {\bf k} \\[1pt] 1 & 1 & 0 \\[1pt] 0 & 1 & 1 \end{array} \right|={\bf i}-{\bf j}+{\bf k}. \]
Because \(\|{\bf i}-{\bf j} +{\bf k}\|=\sqrt{3}\), the vector \[ \frac{1}{\sqrt{3}}({\bf i}-{\bf j}+{\bf k}) \] is a unit vector perpendicular to \({\bf i}+{\bf j}\) and \({\bf j}+{\bf k}\).
example 7
Derive an identity relating the dot and cross products from the formulas \[ \|{\bf u}\times {\bf v}\|=\|{\bf u}\|\|{\bf v}\|\sin \theta\qquad\hskip-2pt{\rm and}\qquad\hskip-2pt {\bf u}\,{\cdot}\, {\bf v}=\|{\bf u}\|\|{\bf v}\|\cos \theta \] by eliminating \(\theta\).
solution Seeing \(\sin \theta\) and \(\cos \theta\) multiplied by the same expression suggests squaring the two formulas and adding the results. We get \[ \|{\bf u}\times {\bf v}\|^2+({\bf u}\,{\cdot}\, {\bf v})^2=\|{\bf u}\|^2\|{\bf v}\|^2(\sin^2\theta+ \cos^2\theta)=\|{\bf u}\|^2\|{\bf v}\|^2, \]
so \[ \|{\bf u}\times {\bf v}\|^2=\|{\bf u}\|^2\|{\bf v}\|^2-({\bf u}\,{\cdot}\, {\bf v})^2. \]
This identity is interesting because it establishes a link between the dot and cross products.
39
Geometry of Determinants
Using the cross product, we may obtain a basic geometric interpretation of \(2\times 2\) and \(3\times 3\) determinants. Let \({\bf a}=a_1{\bf i}+a_2{\bf j}\) and \({\bf b}=b_1{\bf i}+b_2{\bf j}\) be two vectors in the plane. If \(\theta\) is the angle between \({\bf a}\) and \({\bf b}\), we have seen that \(\|{\bf a}\times {\bf b}\|=\|{\bf a}\|\|{\bf b}\| {\mid}{\sin}\, {\theta}{\mid}\) is the area of the parallelogram with adjacent sides a and b. The cross product as a determinant is \[ {\bf a}\times {\bf b}=\left| \begin{array}{@{}c@{\quad}c@{\quad}c@{}} {\bf i} & {\bf j} & {\bf k} \\ a_1 &a_2 & 0 \\ b_1 & b_2 & 0 \end{array} \right| =\bigg| \begin{array} &a_1 & a_2 \\[3pt] b_1 &b_2 \end{array} \bigg|\,{\bf k}. \]
Thus, the area \(\|{\bf a}\times {\bf b}\|\) is the absolute value of the determinant \[ \bigg|\begin{array} &a_1 & a_2\\[3pt] b_1& b_2 \end{array} \bigg| = a_1b_2-a_2b_1. \]
Geometry of \({\hbox{2} {\times} \hbox{2}}\) Determinants
The absolute value of the determinant \(\scriptsize\big|\begin{array}{cc} a_1& a_2 \\ b_1& b_2 \end{array} \big|\) is the area of the parallelogram whose adjacent sides are the vectors \({\bf a}=a_1{\bf i}\,+\,a_2{\bf j}\) and \({\bf b}=b_1{\bf i}\,+\,b_2{\bf j}\). The sign of the determinant is \(+\) when, rotating in the counterclockwise direction, the angle from \({\bf a}\) to \({\bf b}\) is less than \(\pi\).
example 8
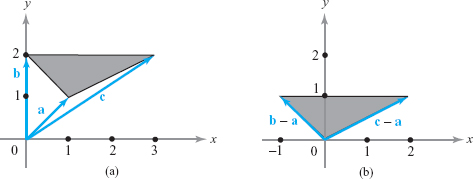
Find the area of the triangle with vertices at the points (1, 1), (0, 2), and (3, 2) (see Figure 1.48).
40
solution Let \({\bf a}={\bf i}+{\bf j},{\bf b}=2{\bf j},\) and \({\bf c}=3{\bf i}+2{\bf j}\). It is clear that the triangle whose vertices are the endpoints of the vectors \({\bf a},{\bf b}\), and \({\bf c}\) has the same area as the triangle with vertices at \({\bf 0},{\bf b}-{\bf a},\) and \({\bf c}-{\bf a}\) (Figure 1.48). Indeed, the latter is merely a translation of the former triangle. Because the area of this translated triangle is one-half the area of the parallelogram with adjacent sides \({\bf b}-{\bf a}=-{\bf i}+{\bf j},\) and \({\bf c}-{\bf a}=2{\bf i}+{\bf j}\), we find that the area of the triangle with vertices (1, 1), (0, 2), and (3, 2) is the absolute value of \[ \frac{1}{2}\left|\ \begin{array} -1 & 1 \\ 2 & 1 \end{array} \right|=-\frac{3}{2}, \] that is, 3/2.
There is an interpretation of determinants of \(3\times 3\) matrices as volumes that is analogous to the interpretation of determinants of \(2\times 2\) matrices as areas.
Geometry of 3 \( \times\) 3 Determinants
The absolute value of the determinant \begin{eqnarray*} D=\left|\begin{array}{ccc} a_1 & a_2 & a_3 \\ b_1& b_2 & b_3 \\ c_1 & c_2 & c_3 \end{array} \right| \end{eqnarray*} is the volume of the parallelepiped whose adjacent sides are the vectors \[ {\bf a}=a_1{\bf i}+a_2{\bf j}+a_3{\bf k}, {\bf b}=b_1{\bf i}+b_2{\bf j}+ b_3{\bf k},\hbox{and}\qquad {\bf c}=c_1{\bf i}+c_2{\bf j}+c_3{\bf k}. \]
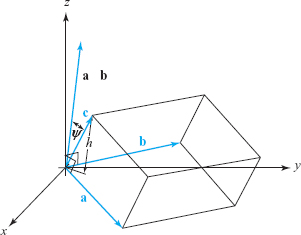
To prove the statement in the preceding box, we refer to Figure 1.49 and note that the length of the cross product, namely, \(\|{\bf a}\times {\bf b}\|\), is the area of the parallelogram with adjacent sides a and b. Moreover, \(({\bf a}\times {\bf b})\,{\cdot}\, {\bf c}=\|{\bf a} \times {\bf b}\|\|{\bf c}\|\cos \psi\), where \(\psi\) is the angle that \({\bf c}\) makes with the normal to the plane spanned by \({\bf a}\) and \({\bf b}\). Because the volume of the parallelepiped with adjacent sides \({\bf a},{\bf b}\), and \({\bf c}\) is the product of the area of the base \(\|{\bf a}\times {\bf b}\|\) and the altitude \(\|{\bf c}\| {\mid}\cos \psi{\mid}\), it follows that the volume is \(|({\bf a}\times {\bf b})\,{\cdot}\, {\bf c})|\). We saw earlier that \(({\bf a}\times {\bf b})\,{\cdot}\, {\bf c}=D\), so the volume equals the absolute value of \(D\).
41
example 9
Find the volume of the parallelepiped spanned by the three vectors \({\bf i}\,+\,3{\bf k},2{\bf i}\,+{\bf j}-2{\bf k},\) and \(5{\bf i}+4{\bf k}\).
solution The volume is the absolute value of \[ \left|\begin{array}{@{}c@{\quad}c@{\quad}r@{}} 1& 0 & 3\\ 2& 1& -2 \\ 5& 0 & 4 \end{array} \right|. \]
If we expand this determinant by minors by going down the second column, the only nonzero term is \[ \bigg| \begin{array} &1& 3\\ 5& 4 \end{array} \bigg|(1)=-11 , \] so the volume equals 11.
Equations of Planes
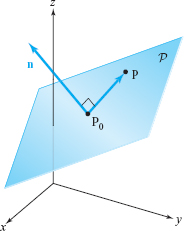
Let \(\cal P\) be a plane in space, \({\rm P}_{\rm 0}=(x_0,y_0,z_0)\) a point on that plane, and suppose that \({\bf n}=A{\bf i}+B{\bf j}+C{\bf k}\) is a vector normal to that plane (see Figure 1.50). Let \({\rm P}\,=\,(x,y,z)\) be a point in \({\mathbb R}^3\). Then P lies on the plane \(\cal P\) if and only if the vector \(\overrightarrow{{\rm P}_{\rm 0}{\rm P}\vphantom{^\prime}}=(x-x_0){\bf i}+(y-y_0){\bf j}+(z-z_0){\bf k}\) is perpendicular to \({\bf n},\) that is, \(\overrightarrow{{\rm P}_{\rm 0}{\rm P}\vphantom{^\prime}}\,{\cdot}\, {\bf n}=0\), or, equivalently, \[ (A{\bf i}+B{\bf j}+C{\bf k})\,\,{\cdot}\,\, [(x-x_0){\bf i}+(y-y_0){\bf j}+(z-z_0){\bf k}]=0. \]
Thus, \[ A(x-x_0)+B(y-y_0)+C(z-z_0)=0. \]
Equation of a Plane in Space
The equation of the plane \({\cal P}\), through \((x_0,y_0,z_0)\) that has a normal vector \({\bf n}=A{\bf i}+B{\bf j}+C{\bf k}\) is \[ A(x-x_0)+B(y-y_0)+C(z-z_0)=0; \] that is, \((x,y,z) \in\) \({\cal P}\) if and only if \[ Ax+By+Cz+D=0, \] where \(D=-Ax_0-By_0-Cz_0.\)
42
The four numbers \(A,B,C,\) and \(D\) are not determined uniquely by the plane \(\cal P\). To see this, note that \((x,y,z)\) satisfies the equation \(Ax+By+Cz+D=0\) if and only if it also satisfies the relation \[ (\lambda A)x+(\lambda B)y+(\lambda C)z+(\lambda D)=0 \] for any constant \(\lambda\neq 0\). Furthermore, if \(A,B,C,D\) and \(A',B',C',D'\) determine the same plane \(\cal P\), then \(A=\lambda A',B=\lambda B' ,C=\lambda C',D=\lambda D'\) for a scalar \(\lambda\). Consequently, \(A,B,C,D\) are determined by \(\cal P\) up to a scalar multiple.
example 10
Determine an equation for the plane that is perpendicular to the vector \({\bf i}\,+\,{\bf j}\,+\,{\bf k}\) and contains the point (1, 0, 0).
solution Using the general form \(A(x-x_0)+B(y-y_0)+C(z-z_0)\,=\,0,\) the plane is \(1(x-1)+1(y-0)+1(z-0)=0\); that is, \(x+y+z=1\).
example 11
Find an equation for the plane containing the three points (1, 1, 1), (2, 0, 0), and (1, 1, 0).
solution Method 1. This is a “brute force” method that you can use if you have forgotten the vector methods. The equation for any plane is of the form \(Ax+By+Cz+D=0\). Because the points (1, 1, 1), (2, 0, 0), and (1, 1, 0) lie in the plane, we have \begin{eqnarray*} \begin{array} &A&+&B&+&C&+&D&=&0,\\[6pt] 2A& & & & &+&D&=&0,\\[6pt] A&+&B& & &+&D&=&0. \end{array} \end{eqnarray*}
Proceeding by elimination, we reduce this system of equations to the form \begin{eqnarray*} 2A+D&=&0\quad (\hbox{second equation})\\ 2B+D&=&0\quad (2\times \hbox{third}-\hbox{second}),\\ C&=&0\quad (\hbox{first}- \hbox{third}). \end{eqnarray*}
Because the numbers \(A,B,C,\) and \(D\) are determined only up to a scalar multiple, we can fix the value of one of them, say \(A=1\), and then the others will be determined uniquely. We get \(A=1\), \(D=-2\), \(B=1,C=0\). Thus, an equation of the plane that contains the given points is \(x+y-2=0\).
Method 2. Let \({\rm P} =(1,1,1),{\rm Q}=(2,0,0),{\rm R}=(1,1,0)\). Any vector normal to the plane must be orthogonal to the vectors \(\overrightarrow{\rm QP\vphantom{^\prime}}\) and \(\overrightarrow{\rm RP\vphantom{^\prime}}\), which are parallel to the plane, because their endpoints lie on the plane. Thus, \({\bf n}=\overrightarrow{\rm QP\vphantom{^\prime}}\times \overrightarrow{\rm RP\vphantom{^\prime}}\) is normal to the plane. Computing the cross product, we have \[ {\bf n}=\left|\begin{array}{@{}r@{\quad}c@{\quad}c@{}} {\bf i}& {\bf j}& {\bf k} \\ -1 & 1&1 \\ 0 &0 & 1 \end{array} \right|={\bf i}+{\bf j}. \]
Because the point (2, 0, 0) lies on the plane, we conclude that the equation is given by \((x-2)+(y-0)+0\,{\cdot}\, (z-0)=0\); that is, \(x+y-2=0\).
Two planes are called parallel when their normal vectors are parallel. Thus, the planes \(A_{1}x+B_{1}y+C_{1}z+D_{1} = 0\) and \(A_{2}x+B_{2}y+C_{2}z+D_{2} = 0\) are parallel
43
when n\(_{1} = A_{1} {\bf i} + B_{1} {\bf j} + C_{1}{\bf k}\) and n\(_{2} = A_{2} {\bf i} + B_{2} {\bf j} + C_{2}{\bf k}\) are parallel; that is, \(n_{1}=\sigma n_{2}\) for a constant \(\sigma\). For example, the planes \[ x - 2y+z = 0 \hbox{and} {-}2x + 4y - 2z = 10 \] are parallel, but the planes \[ x - 2y+z = 0 \hbox{and} 2x - 2y+z = 10 \] are not parallel.
Distance: Point to Plane
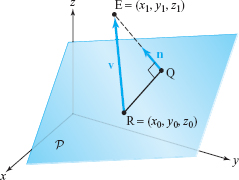
Let us now determine the distance from a point E \(=(x_1,y_1,z_1)\) to the plane \({\cal P}\) described by the equation \(A(x-x_0)+B(y-y_0)+C(z-z_0)=Ax+By+Cz+D=0\). To do so, consider the unit normal vector \[ {\bf n}=\frac{A{\bf i}+B{\bf j}+C{\bf k}}{\sqrt{A^2+B^2+C^2}}, \] which is a unit vector normal to the plane. Drop a perpendicular from E to the plane and construct the triangle REQ shown in Figure 1.51. The distance \(d=\|\overrightarrow{\rm EQ\vphantom{^\prime}}\|\) is the length of the projection of \({\bf v}=\overrightarrow{\rm RE\vphantom{^\prime}}\) (the vector from R to E) onto \({\bf n}\); thus, \begin{eqnarray*} \hbox{Distance}=|{\bf v}\,{\cdot}\, {\bf n}| &=& |[(x_1-x_0) {\bf i}+(y_1-y_0){\bf j}+(z_1-z_0){\bf k}]\,{\cdot}\, {\bf n}|\\[6pt] &=&\frac{|A(x_1-x_0)+B(y_1-y_0)+C(z_1-z_0)|}{\sqrt{A^2+B^2+C^2}}. \end{eqnarray*}
If the plane is given in the form \(Ax+By+Cz+D=0\), then for any point \((x_0,y_0,z_0)\) on it, \(D=-(Ax_0+By_0+Cz_0)\). Substitution into the previous formula gives the following:
Distance from a Point to a Plane
The distance from \((x_1,y_1,z_1)\) to the plane \(Ax+By+Cz+D=0\) is \[ \hbox{Distance}=\frac{|Ax_1+By_1+Cz_1+D|}{\sqrt{A^2+B^2+C^2}}. \]
44
example 12
Find the distance from \({\rm Q}=(2,0,-1)\) to the plane \(3x-2y\,+\,8z\,+\,1\,=\,0\).
solution We substitute into the formula in the preceding box the values \(x_1\,{=}\,2 y_1=0,z_1=-1\) (the point) and \(A=3,B=-2,C=8,D=1\) (the plane) to give \[ \hbox{Distance} =\frac{|3\,{\cdot}\, 2+(-2)\,{\cdot}\, 0+8(-1)+1|}{\sqrt{3^2+(-2)^2+8^2}}= \frac{|{-}1|}{\sqrt{77}}=\frac{1}{\sqrt{77}}. \]
Historical Note
The Origins of the Vector, Scalar, Dot, and Cross Products
QUADRATIC EQUATIONS, CUBIC EQUATIONS, AND IMAGINARY NUMBERS. We know from Babylonian clay tablets that this great civilization possessed the quadratic formula, enabling them (in verbal form) to solve quadratic equations. Because the concept of negative numbers had to wait until the sixteenth century to see the light of day, the Babylonians did not consider either negative (or imaginary) solutions.
With the Renaissance and the rediscovery of ancient learning, Italian mathematicians began to wonder about the solutions of cubic equations, \(x^{3} + a\,x^{\,2} + b\,x + c\, = 0\), where a, b, and c are positive numbers.
Around 1500, Scipione del Ferro, a professor in Bologna (the oldest European university), was able to solve cubics of the form \(x^{3} + b\,x = c\,\), but kept his discovery secret. Before his death, he passed his formula to his successor, Antonio Fior, who for a while also kept the formula to himself. It remained a secret until a brilliant, self-taught mathematician named Nicolo Fontana, also known as Tartaglia (the stammerer), appeared on the scene. Tartaglia claimed he could solve the cubic, and Fior felt he needed to protect the priority of del Ferro, and so in response challenged Tartaglia to a public competition.
We are told that Tartaglia was able to solve all of the thirty cubic equations posed by Fior. Amazingly, some scholars believe that Tartaglia discovered the formula for solutions to \(x^{3} + c\,x = d\,\) only days before the contest was to take place.
The greatest mathematician of the sixteenth century, Gerolamo Cardano (1501–1576)—a Renaissance scholar, mathematician, physician, and fortuneteller—gave the first published solution of the general cubic. Although born of modest means, he (like Tartaglia) rose, through effort and natural brilliance, to great fame. Cardano is the author of the first book on games of chance (marking the beginning of modern probability theory) and also of Ars Magna (the Great Art), which marks the beginning of modern algebra. It was in this book that Cardano published the solution to the general cubic \(x^{3} + a\,x^{\,2} + b\,x + c\, = 0\). How did he get it?
While working on his algebra book, and aware that Tartaglia was able to solve forms of cubic, Cardano, in 1539, wrote to Tartaglia asking for a meeting. After some cajoling, Tartaglia agreed. It was at this meeting that, in exchange for a pledge of secrecy (and we know how these generally go), Tartaglia revealed his solution, from which Cardano was able to derive a solution to the general equation, which then appeared in Ars Magna. Feeling betrayed, Tartaglia led a scathing attack on Cardano, leading to a small soap opera.
What is important for us, at the moment, is that as a consequence of the method of solution, something very strange occurred. Consider the cubic \(x^{3}- 15x = 4\). Its only positive root is 4. However, the Tartaglia–Cardano solution
45
formula yields \[ x=\sqrt[3]{2+\sqrt{-121}}+\sqrt[3]{2-\sqrt{-121}}\tag{3} \] as the positive root. Thus, this number must be equal to 4. Yet this must be nonsense, because inside the cube root we are taking the square root of a negative number—at the time, an absolute impossibility. This was a real shock. Over 100 years later, in 1702, when Leibniz, codiscoverer of calculus, showed the great Dutch scientist Christian Huygens the formula \[ \sqrt{6}=\sqrt{1+\sqrt{-3}}+\sqrt{1-\sqrt{-3}}\tag{4} \]
Huygens was completely flabbergasted, and remarked that this equality “defies all human understanding.” (Try, informally, to verify both formulas (1) and (2) for yourself.)
Whether nonsense or not, Tartaglia and Cardano’s formula forced mathematicians to confront square roots of negative numbers (or imaginary numbers, as they are called today).
THE MATURING OF COMPLEX NUMBERS. For well over two centuries, numbers like \(i=\sqrt{-1}\) were looked at with great suspicion. The square root of any negative number can be written in terms of \(i\); for example, \(\sqrt{-a}\, = \sqrt{\hbox{(}a\,\hbox{)}\hbox{(}-1\hbox{)}} = \sqrt{a}\,\sqrt{-1}\). In the middle of the eighteenth century, the Swiss mathematician Leonhard Euler connected the universal cosmic numbers \(e\) and \(\pi\) with the imaginary number \(i\). Whatever \(i\) was or meant, it necessarily follows that \[ e^{\;\pi\kern-1pti} = -1\hbox{,} \] that is, \(e\)“raised to the power \(\pi\kern-1pti\) equals \(-1\).” Thus, these cosmic numbers, reflecting perhaps some deeper mystery, are in fact connected to each other by a very simple formula.
At the beginning of the nineteenth century, the German mathematician Karl Friedrich Gauss was able to prove the fundamental theorem of algebra, which says that any \(n\,\)th-degree polynomial has \(n\) roots (some or all of which may be imaginary; that is, the roots have the form \(a\, + bi\), where, as earlier, \(i=\sqrt{-1}\) and where \(a\,\) and \(b\,\) are real numbers).
By the middle of the nineteenth century, the French mathematician Augustin-Louis Cauchy and the German mathematician Bernhard Riemann had developed the differential calculus for functions of one complex variable. An example of such a function is \(F \hbox{(}z\hbox{)}=z^{n}\), where \(z=a \,\,{+}\, \)bi. In this case, the usual formula for the derivative, \(F^{\kern1pt\prime}\hbox{(}z\hbox{)}\,{=}\,\)nz\(^{\,n -1}\), still holds. However, by introducing imaginary numbers, Cauchy was able to evaluate “real integrals” that heretofore could not be evaluated. For example, it is possible to show that \[ \int^\infty_0\frac{\sin x}{x}\ dx=\frac{\pi}{2} \] and that \[ \int^\pi_0 \log\sin x\, dx=-\pi\log 2\hbox{.} \] These were stunning results.
46
In summary, the solution of the cubic equation, the fundamental theorem of algebra, and the evaluation of real integrals proved how valuable it was to consider imaginary numbers \(a\,{+}\,\)bi, even though they were not (at least not yet) on terra firma. Did they really exist or were they simply phantoms of our imagination, and thus truly imaginary?

HAMILTON’S DEFINITION OF COMPLEX NUMBERS. Many mathematicians after Cardano made important contributions to imaginary (or complex) numbers, including Argand, Wessel, and Gauss—all of whom represented them geometrically. However, the modern, intellectually rigorous definition of a complex number is due to the great Irish mathematician William Rowan Hamilton (see Figure 1.52). After Newton, who created the vector concept through his invention of the notion of force, Hamilton was, beyond any doubt, the most important and singular figure in the development of vector calculus. It was Hamilton who gave us the terms vector and scalar quantity.
William Rowan Hamilton was born in Dublin, Ireland, at midnight on August 3, 1805. In 1823, he entered Trinity College, Dublin. His university career, by any standard, was phenomenal. By his third year, Trinity offered him a professorship, the Andrew’s Chair of Astronomy, and the State named him Royal Astronomer of Ireland. These honors were based on his theoretical prediction (in 1824) of two entirely new and unexpected optical phenomena, namely, internal and external conical refraction.
By 1827 he had become interested in imaginary numbers. He wrote that “the symbol \(\sqrt{-1}\) is absurd, and denotes an impossible extraction\(,\ldots\)” He set out to put the idea of a complex number on a firm logical foundation. His solution was to define a complex number \(a\, + b\,i\) as a point (\(a, b\,\)) in the plane \({\mathbb R}^{2}\), much as we do today. Thus, the imaginary number bi for Hamilton was simply the point (0, \(b\)) on the \(y\) axis. The difference between complex numbers and the Cartesian plane was that Hamilton followed the proforma multiplication of complex numbers: \[ \hbox{(}a + b\,i\hbox{)(}c + d\,i\hbox{)} = \hbox{(}a\,c - b\,d\;\hbox{)} + \hbox{(}a\,d + b\,c\,\hbox{)}i\hbox{,} \] and defined a new multiplication on the complex plane: \[ \hbox{(}a\,, b\,\hbox{)} \cdot \hbox{(}c\,, d\,\hbox{)} = \hbox{(}a\,c - b\,d\,, a\,d + b\,c\,\hbox{)}. \]
Thus, \(i=\sqrt{-1}\) just disappears into the point (0, 1), and the mystery and confusion over complex numbers disappears along with it.
FROM COMPLEX NUMBERS TO QUATERNIONS. From Hamilton’s interpretation, complex numbers are nothing more than the extension of real numbers into a new dimension, two dimensions. Hamilton, however, also did fundamental work in mechanics, and he knew well that two dimensions were too limiting for the space analysis necessary for understanding the physics of the three-dimensional world. Therefore, Hamilton set out to find a triplet system; that is, an acceptable1 multiplication scheme on points (\(a\,\), \(b\,\), \(c\,\)) in \({\mathbb R}^{3}\), or, as it were, on vectors \(a\,\hbox{i} + b\,\hbox{j }+ c\, \hbox{k}\).
47
By 1843, Hamilton realized that his quest was hopeless. But then, on October 16, 1843, Hamilton discovered that what he could not achieve for \({\mathbb R}^{3}\) he could achieve for \({\mathbb R}^{4}\); he discovered quaternions, an entirely new number system.
Hamilton2 had realized that the multiplication he had been searching for could be introduced on 4-tuples (\({a}\,\), \({b}\,\), \({c}\,\), \({d}\,\)), which he had denoted by \[ a+b\,\hbox{i} + c\,\hbox{j} + d\,\hbox{k}. \]
The \(a\) was called the scalar part and \(b\;\hbox{i} + c\,\hbox{j} + d\,\hbox{k}\) was called the vector part, which in reality, as with complex numbers, meant the point (a\({\hbox{,}}\) b\({\hbox{,}}\) c\({\hbox{,}}\) d) in \({\mathbb R}^{4}\). The multiplication table he introduced was \[ \begin{array}{@{}c@{}} \hbox{ij} = \hbox{k} = -\hbox{ji}\\[4pt] \hbox{ki} = \hbox{j} = -\hbox{ik}\\[4pt] \hbox{jk} = \hbox{i} = -\hbox{kj}\\[4pt] \hbox{i}^{2} = \hbox{j}^{2} = \hbox{k}^{2} = \hbox{ijk}=-1. \end{array} \]
Hamilton continued to passionately believe in his quaternions until the end of his life. Unfortunately, historical development went in another direction.
The first step away from the quaternions was in fact taken by a firm believer in the importance of quaternions, namely, Peter Guthrie Tait, who was born in 1831 near Edinburgh, Scotland. In 1860, Tait was appointed to the Chair of Natural Philosophy at Edinburgh University, where he remained until his death in 1901. In 1867, he wrote his Elementary Treatises on Quaternions, a text stressing physical applications. His third chapter was most significant. It was here that Tait looked at the quaternionic product of two vectors: \[ \hbox{v} = a\,\hbox{i }+ b\,\hbox{j} + c\,\hbox{k}\qquad \hbox{and}\qquad \hbox{w} = a\,' \hbox{i} + b\,' \hbox{j} + c\,' \hbox{k.} \]
Then the product vw, as defined by Hamilton, yields: \begin{eqnarray*} && \hbox{(}a\,\hbox{i} + b\,\hbox{j} + c\,\hbox{k}\hbox{)} \hbox{(}a\,' \hbox{i} + b\,' \hbox{j} + c\,' \hbox{k}\hbox{)} \\ &&\qquad = -\hbox{(}\hbox{aa}\,' + \hbox{bb}' + \hbox{cc}\, '\hbox{)} + \hbox{(} b\,c\, ' - c\,b\,'\hbox{)}\hbox{i} + \hbox{(}a\,c\,' - c\,a\, '\hbox{)}\hbox{j} + \hbox{(}a\,b\, ' - b\,a\,'\hbox{)} \hbox{k} \end{eqnarray*} or, in modern form: \[ \hbox{vw} = -\hbox{(}\hbox{v}\ { \cdot}\ \hbox{w}\hbox{)} + \hbox{v} \times \hbox{w}\hbox{,} \] where \({ \cdot}\) is the modern dot or inner product of vectors and \(\times\) is the cross product. Tait discovered the formulas \[ \hbox{v}\ { \cdot}\ \hbox{w }= \| \hbox{v}\| \| \hbox{w}\| \cos \theta \qquad \hbox{and}\qquad \| \hbox{v} \times \hbox{w}\| =\| \hbox{v}\| \| \hbox{w}\| \sin\theta\hbox{,} \] where \(\theta\) is the angle formed by v and w. Moreover, he showed that v \(\times \) w was orthogonal to v and w, therefore giving a geometric interpretation of the quaternionic product of two vectors.
48
This began the move away from the study of quaternions and back to Newton’s vectors, with the quaternionic product eventually being replaced by two separate products, the inner product and the cross product.
By the way, you might wonder why Hamilton did not at first discover the cross product, since it is a product on \({\mathbb R}^{3}\). The reason is that it did not have a fundamental property that he required—namely, it was not associative:3 \[ 0 = \hbox{(}\hbox{i} \times \hbox{i}\hbox{)} \times \hbox{k} \ne \hbox{i} \times \hbox{(}\hbox{i} \times \hbox{k}\hbox{)} = -\hbox{k}. \]
Remarkably, Euler discovered the cross product in component form in 1750, and three years before Hamilton, Olinde Rodrigues also discovered a form of quartenionic multiplication.
THE MOVE AWAY FROM QUATERNIONS. The scientists ultimately responsible for the demise of quaternions were James Clerk Maxwell (see Figure 1.53), Oliver Heaviside, and Josiah Willard Gibbs, a founder of statistical mechanics. In the 1860s, Maxwell wrote down his monumental equations of electricity and magnetism. No vector notation was used (it did not exist). Instead, Maxwell wrote out his equations in what we would now call “component form.” Around 1870, Tait began to correspond with Maxwell, piquing his interest in quaternions.
In 1873, Maxwell published his epic work, Treatise on Electricity and Magnetism. Here (as we shall do in Chapter 8), Maxwell wrote down the equations of the electromagnetic field using quaternions, thus motivating physicists and mathematicians alike to take a closer look at them. From this manuscript many have concluded that Maxwell was a supporter of the “quaternionic approach” to physics. The truth, however, is that Maxwell was reluctant to use quaternions. It was Maxwell, in fact, who began the process of separating the vector part of a product of two quaternions (the cross product) from its scalar part (the dot product).
It is known that Maxwell was troubled by the fact that the scalar part of the “square” of a vector (v) was always negative (\(-\)v \({ \cdot}\) v), which in the case of a velocity vector could be interpreted as negative kinetic energy—an unacceptable idea!
It was Heaviside and Gibbs who made the final push away from quaternions. Heaviside, an independent researcher interested in electricity and magnetism, and Gibbs, a professor of mathematical physics at Yale, almost simultaneously— and independently—created our modern system of vector analysis, which we have just started to study.
49
In 1879, Gibbs taught a course at Yale in vector analysis with applications to electricity and magnetism. This treatise was clearly motivated by the advent of Maxwell’s equations, which we will be studying in Chapter 8. In 1884, he published his Elements of Vector Analysis, a book in which all the properties of the dot and cross products are fully developed. Knowing that much of what Gibbs wrote was in fact due to Tait, Gibbs’s contemporaries did not view his book as highly original. However, it is one of the sources from which modern vector analysis has come into existence.

Heaviside was also largely motivated by Maxwell’s brilliant work. His great Electromagnetic Theory was published in three volumes. Volume I (1893) contained the first extensive treatment of modern vector analysis.
We all owe a great debt to E. B. Wilson’s 1901 book Vector Analysis: A Textbook for the Use of Students of Mathematics and Physics Founded upon the Lectures of J. Willard Gibbs. Wilson was reluctant to take Gibbs’s course, because he had just completed a full-year course in quaternions at Harvard under J. M. Pierce, a champion of quaternionic methods; but he was forced by a dean to add the course to his program, and he did so in 1899. Wilson was later asked by the editor of the Yale Bicentennial Series to write a book based on Gibbs’s lectures. For a picture of Gibbs and for additional historical comments on divergence and curl, see the Historical Note in Section 4.4.